ChatGPT ylioppilaskokeessa

Pääsisikö ChatGPT ylioppilaaksi?

Sitähän on puitu viime kuukaudet kaikissa kahvi- ja baaripöydissä (ainakin nörttipiireissä), miten hurjasti ChatGPT:n kaltaiset suuret kielimallit ovat kehittyneet, ja vievätkö ne meiltä kohta kaikki siistit sisätyöt. Yksi yleinen argumentti näissä keskusteluissa on, että vaikka kielimalli voi tuottaa häkellyttävän uskottavaa tekstiä, se on pohjimmiltaan vain seuraavan sanan ennustin, vähän kuin puhelimen ennustava tekstinsyöttö jolla on taustallaan muutama kertaluokka enemmän dataa ja laskentatehoa kuin puhelimessa. Siksi se on vain stokastinen papukaija, joka papattaa sanoja ymmärtämättä mitään todellisuudesta. Toki papukaijalla voidaan korvata joku keskinkertainen keskitason johtaja, jonka tuottama sisältömarkkinointistrategia tai monitilatoimistosuunnitelma on yhtä lailla irrallaan todellisuudesta ja siksi mahdoton erottaa papukaijan tuotoksista, mutta eihän se osaa tehdä oikeaa ajatustyötä. Varsinkin laskennossa ChatGPT on tunnetusti huono, joten ehkäpä laskento onkin se ihmisyyden kova ydin, jota mikään papukaija-armeija ei voi koskaan saavuttaa.

Vai voiko? Kokeillaan.

Laskentoakin on monenlaista, mutta sen eräänlainen huipentuma on ylioppilastutkinnon matematiikan koe, tietysti laaja oppimäärä. Matematiikanopettajien ikuinen valitus on, että heidän nuoruudessaan kurssi oli vaikea ja nykynuorilla on liian helppoa, joten seuraan tätä ja valitsen ChatGPT:n testaamiseen oman nuoruuteni koitoksen, vuoden 1995 ylioppilaskokeen. Koska silloin sai käyttää laskinta, annetaan myös ChatGPT:n käyttää eräänlaista laskinta: maksullinen ChatGPT Plus (GPT-4) sisältää Advanced Data Analysis -moodin, jossa se voi kirjoittaa Python-koodia ja suorittaa sitä. Koska en jaksa kirjoittaa tehtäviä koneelle, otan niistä ruutukaappaukset ja annan GPT-4V:n tulkita ne tekstiksi.

Harmillisesti Pythonin suorittaminen ja kuvien tulkitseminen eivät ole mahtuneet samaan malliin, joten päädyin erinäisten esikokeilujen jälkeen käyttämään ChatGPT:tä kaksi kertaa kunkin tehtävän kohdalla: ensiksi tehtävän tulkitsemiseen skannauksesta (GPT-4V) ja toiseksi sen ratkaisemiseen (GPT-4 Advanced Data Analysis). Vaikka ChatGPT osaa lukea suomea ihan kohtalaisesti, sen päättelykyky on tuntunut paremmalta englanniksi, joten annetaan sen kääntää tehtävät ja vastata äidinkielellään.

Arvostelussa nojaudun kahteen löytämääni lähteeseen: kirjaan Kangasaho, Piri, Taavitsainen: Pitkän matematiikan ylioppilaskokeet 1991-1999, WSOY 1999, ja Aatos Lahtisen kirjoitukseen Matematiikan ylioppilaskirjoitus keväällä 1995, Dimensio 1/1996. Lahtinenkin tulee vahvistaneeksi, että nykynuorten helpompi aikakausi on alkanut välittömästi tämän kirjoituskerran jälkeen: keväällä 1995 noudatettiin nimittäin viimeisen kerran vuoden 1947 ylioppilastutkintoasetusta. Hän myös esittää Orwellia mukailevan mietteen matematiikan merkityksestä:

Joka hallitsee matematiikan nykyisyyden, hallitsee ihmiskunnan tulevaisuuden.

Tässä on siis tekoälyllä paljon pelissä.

Koeasetelma

Otin tehtäväkokoelmasta ruutukaappauksia ja annoin GPT-4V:lle. Kielimalleille voi ja kannattaa antaa kehotteita (prompt), ja kuvan tulkintavaihetta ohjeistin näin:

The image contains a math problem, or possibly two problems labeled (a) and (b). Translate the problem into English as precisely as possible. Do not attempt to solve the problem or comment on it in any way.

Ratkaisuvaiheen mallille (GPT-4 Advanced Data Analysis) esitin edellisen vaiheen tuottaman käännöksen ja tällaisen ohjeen:

Here is a math problem, or possibly two problems labeled (a) and (b), in which case you should pick only the one that you are more confident in being able to solve. Start your answer with a heading “THINKING” and identify what is being asked, what the inputs are, and what mathematical concepts are related. Then under a heading “SOLUTION” provide a complete solution. If a numerical answer is required, give an exact value if possible, and an approximation.

Ylioppilaskokeessa kokelaalla oli ainakin ennen nykyajan tietoteknisiä hömpötyksiä lupa kirjoittaa muistiinpanoja ja kokeiluja suttupaperille, ja saman mahdollisuuden tarjoaminen ChatGPT:lle tuntuu reilulta. Esikokeilujen perusteella tämä myös auttaa ainakin joissakin tehtävissä.

En toista seuraavassa kaikkea ChatGPT:n tulostetta vaan siteeraan vain käännöksen englanniksi ja ratkaisun kiinnostavimmat osat. Täydet ratkaisut jätän liitteeseen.

Tehtävä 1: epäyhtälö

“Solve the inequality $|2 - x| < \sqrt{x - 2}$.”

Huonosti alkaa - kerroin 2 jää huomaamatta, joten tekoäly ratkaisee väärän epäyhtälön. Ehkä ihmiskokelaskin voisi tehdä vastaavan huolimattomuusvirheen, mutta silloin heräisi epäilys virheen tarkoitushakuisuudesta: ratkaisun osana tarvittava toisen asteen yhtälö muuttuu helpommaksi ratkaista tekijöihin jakamalla.

Step 1: Identify the domain

Both the absolute value and the square root functions have restrictions on their domain.

• The absolute value function $|2 - x|$ is defined for all real numbers $x$.
• The square root function $\sqrt{x - 2}$ is defined for $x \geq 2$.

Ensimmäinen huomio ei ole ihan oikein: itseisarvofunktio on kyllä määritelty kaikille reaaliluvuille. ChatGPT huomaa sen heti mutta jättää vastaukseen tällaiset ristiriitaiset väittämät. Erinäisten vaiheiden jälkeen päästään lopputulokseen, jonka olennainen sisältö on tässä:

[Step 3] Scenario 1: $x > 2$

Squaring both sides to eliminate the square root: The inequality $(x - 2)(x - 3) < 0$ holds when $2 < x < 3$.

Virheellisen epäyhtälön ChatGPT ratkaisee sinänsä oikein ja muistaa ottaa huomioon myös neliöjuuren reaalisuusehdon, joka Lahtisen mukaan jäi monilta huomaamatta. Epäyhtälön ratkaisun perustelut ovat myös riittävät, vaikka tapaustarkastelu on ehkä vähän turhan detaljoitu, joten annan kriittisestä virheestä huolimatta 2 pistettä.

Tehtävä 2: laivamatka

Ships A and B travel the same round trip such that A travels both the outbound and return trip at a speed of 18 knots, while B travels the outbound trip at 20 knots and the return trip at 16 knots. Which of the ships completes the round trip faster? How many percent more time does the slower ship take? One knot is 1.85 km/h.

Tämä käännös näyttää oikealta. Ratkaisussa on paljon askelia, joiden numerointi vähän horjuu, mutta seuraavassa olennaisimmat.

Step 3: Find the total time taken by each ship for the round trip

• Time taken by Ship A for the round trip: $2 \times \frac{d}{33.3} = \frac{2d}{33.3}$
• Time taken by Ship B for the round trip: $\frac{d}{37} + \frac{d}{29.6}$

Step 5: Percentage More Time Taken by the Slower Ship

To find out how much more time the slower ship (Ship B) takes, we can use the formula: We can substitute the expressions for the times taken by both ships into this formula to find the answer.

Tässä kohtaa ChatGPT laskee Pythonin sympy-paketilla tuloksen 1,24999999999998, jonka se pyöristää:

Step 5: Percentage More Time Result

The simplified expression for the percentage more time taken by Ship B is approximately $1.25\%$.

Thus, Ship A completes the round trip faster, and Ship B takes approximately $1.25\%$ more time to complete the round trip.

Käännös meni oikein, ja ratkaisukin näyttää pääpiirteissään oikealta. ChatGPT muuntaa nopeudet solmuista kilometreiksi tunnissa, mitä ei tarvitsisi tehdä. Vähennän turhasta likiarvon käytöstä pisteen, joten kokelas saa 5 pistettä.

Tehtävä 3: pilkottu kuutio

1. Show that for every $k = 1, 2, 3, ...$, the number $k^3 + k$ is even.

2. A cube is divided into sixty-four equally sized smaller cubes. What is the edge length (cm) of these smaller cubes when the original cube’s volume is 1.00 liters?

Tehtävän (b) vastaus on pitkä ja yksityiskohtainen, mutta onneksi lopussa on tiivistelmä:

Summary

The edge length of the smaller cubes, when the original cube of volume 1.00 liters is divided into 64 equally sized smaller cubes, is $2.5 \, \text{cm}$.

Ratkaisu on oikea ja siis 6 pisteen arvoinen. Saman vaihtoehdon olivat valinneet myös useimmat ihmiskokelaat ja saaneet keskimäärin 5,44 pistettä, joten tämä oli helppo tehtävä.

Tehtävä 4: pinta-ala

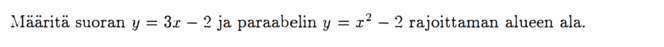
Determine the area bounded by the line $y = 3x - 2$ and the parabola $y = x^2 - 2$.

ChatGPT ratkaisee aivan oikein käyrien leikkauspisteet ja selvittää, kumpi käyrä kulkee ylempänä:

Step 1: Find the Points of Intersection

To find the points where the line and the parabola intersect, we set $y = 3x - 2$ equal to $y = x^2 - 2$ and solve for $x$: $$3x - 2 = x^2 - 2$$ Simplifying, we get: $$\begin{gather} x^2 - 3x = 0 \\ x(x - 3) = 0 \\ x = 0 \quad \text{or} \quad x = 3 \end{gather}$$ The points of intersection are at $x = 0$ and $x = 3$.

Step 2: Determine Which Curve is Above the Other

We need to determine which curve is above the other between $x = 0$ and $x = 3$. We can pick any point in that interval, say $x = 1$, and evaluate both functions: $$ y_{\text{line}}(1) = 3 \cdot 1 - 2 = 1 \\ y_{\text{parabola}}(1) = 1^2 - 2 = -1 $$ Since $y_{\text{line}}(1) > y_{\text{parabola}}(1)$, the line is above the parabola between $x = 0$ and $x = 3$.

Sitten saadaan ihan oikea integraali, mutta ratkaisu tapahtuu ”laskimella”:

Step 3: Calculate the Area

The area between the curves from $x = 0$ to $x = 3$ is given by the integral: $$ \text{Area} = \int_{0}^{3} [(3x - 2) - (x^2 - 2)] \, dx $$ Calculating this integral:

Tässä kohti ChatGPT syöttää integrointitehtävän Pythoniin ja saa vastauksen:

The area between the line $y = 3x - 2$ and the parabola $y = x^2 - 2$ is $\frac{9}{2}$ or approximately $4.5$ square units.

Vastaus 9/2 on oikein eikä 4,5 ole edes likiarvo vaan tarkka, mutta integraalifunktio jää esittämättä. Saakoon 3 pistettä, koska kyllä se integraalifunktio olisi ollut syytä kirjoittaa auki.

Tehtävä 5: käyrän tangentit

1. Determine the points on the curve $y = x^3 - 2x^2 + x - 1$ where the tangents to the curve intersect the x-axis at a 45° angle.

2. The shore plan specifies that one cannot build within 100 m closer to the shore. In the plan area, there is an equilateral triangle-shaped island with a surface area of 5.00 ha. Can construction be allowed on it?

I'll focus on solving problem (a).

Step 1: Find the Derivative

First, let's find the derivative of $ y = x^3 - 2x^2 + x - 1 $ to get the equation of the tangent line at any point $(x, y)$ on the curve. $$ y' = \frac{d}{dx}(x^3 - 2x^2 + x - 1) $$

Tässä välissä käytetään taas Pythonia ja saadaan oikea derivaatta:

The derivative $$ y' = 3x^2 - 4x + 1. $$

Step 2: Relate 45° Angle to Slope

A line making a 45° angle with the x-axis has a slope of $ \tan(45^\circ) = 1$.

Step 3: Solve for the Points

We need to find the points $(x, y)$ where $y' = 1$.

Ratkaisu löytyy Pythonin avulla:

Therefore, the points on the curve $y = x^3 - 2x^2 + x - 1$ where the tangents intersect the x-axis at a 45° angle are $(0, -1)$ and $\left( \frac{4}{3}, -\frac{23}{27} \right)$.

ChatGPT valitsi tehtävän (a) ja ratkaisi sen samoin kuin malliratkaisu, joten se saa 6 pistettä. Derivaatta tuli kylläkin Pythonin avulla, mutta luulen ettei ihmiskokelaaltakaan olisi vaadittu derivoinnin välivaiheiden perustelua.

Dimensiossa keskusteltiin myöhemmin, olisiko kulmakertoimen $1=\tan 45^\circ$ lisäksi pitänyt käsitellä kulmakerroin $-1$, jonka suuntainen suora toki myös muodostaa 45 asteen kulman x-akselin kanssa. Tällaisia tangentteja tehtävän käyrällä ei ole, minkä olisi voinut helpohkosti todistaa. Negatiivisen kulmakertoimen jättämisestä pois ei kuitenkaan kokeessa sakotettu. (Kevään 1995 matematiikan yo-kirjoitusten jälkipyykkiä, Hannu Korhonen ja Heikki Höijer, Dimensio 2/1996.)

Tehtävä 6: kolmiulotteinen kolmio

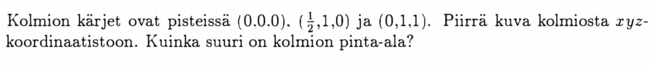
The vertices of the triangle are at points (0,0,0), (1/2,1,0) and (0,1,1). Draw a picture of the triangle in the xyz-coordinate system. How large is the surface area of the triangle?

ChatGPT:n Pythonilla tuottama kuva on yllättävän huono:

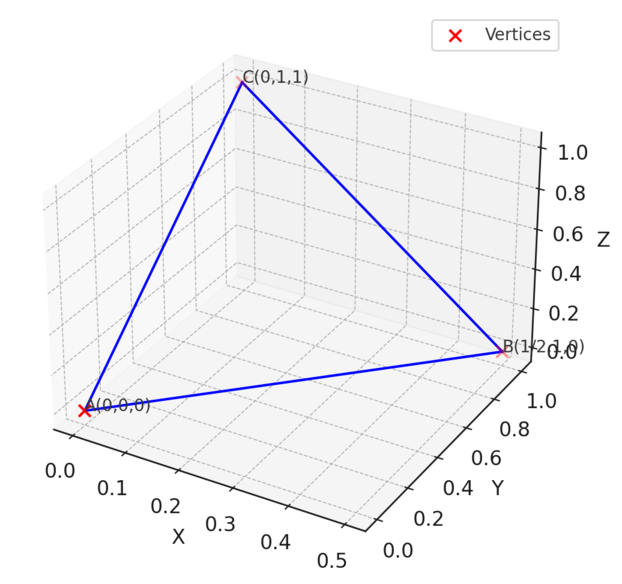
Onhan siinä kolmio, mutta sen kärkipisteet eivät ihan osu oikeisiin koordinaatteihin. Merkintöjä on hankala lukea ja $x$-akselin olisi saanut skaalata niin, että kolmio ei näyttäisi aivan noin symmetriseltä.

Pinta-alan ChatGPT laskee kätevästi ristitulon avulla mutta ilmoittaa tuloksen likiarvon:

First, we find the vectors $\vec{AB}$ and $\vec{AC}$: $$ \vec{AB} = B - A \goodbreak= (1/2, 1, 0) - (0, 0, 0) \goodbreak= (1/2, 1, 0)\\ \vec{AC} = C - A \goodbreak= (0, 1, 1) - (0, 0, 0) \goodbreak= (0, 1, 1) $$ Then, we find the cross product $\vec{AB} \times \vec{AC}$: $$ \vec{AB} \times \vec{AC} = \begin{pmatrix} i & j & k \\ 1/2 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix} $$ Finally, we find the magnitude of the cross product and use it to find the area of the triangle.

[Kokelas näpyttelee kiivaasti laskinta…]

The surface area of the triangle is $0.6123724356957945$ square units, which can be approximated as $0.6124$ square units.

ChatGPT takeltelee vähän ristitulon muistisäännön kanssa: kyseessä on determinantti eikä matriisi. Sakotan likiarvon käytöstä pisteen ja kuvan puutteista toisen, jäljelle jää 4 pistettä.

Tehtävä 7: osittaisintegrointi

1. An investor can deposit capital at 4.60% interest for the entire year or at 4.40% interest for half a year and then with the accumulated amount at p% interest for the remainder of the year. If all percentages p between [4.00, 4.90] are equally likely, what is the probability that the latter method is more advantageous?

2. Functions f and g have continuous derivatives in the interval [a, b]. Derive the partial integration formula: ∫ from a to b of f’g dx = f(b)g(b) - f(a)g(a) - ∫ from a to b of fg’ dx.

ChatGPT tekee käännösvirheen: osittaisintegrointi on englanniksi integration by parts. Ehkä tämän takia se päätyy hyvin sekavaan ratkaisuun, jossa se on johtavinaan kysytyn ”osittaisen integroinnin” (partial integration) kaavan tunnetusta ”osittaisintegroinnin” (integration by parts) kaavasta, joka on ihan sama kaava määräämättömille integraaleille. Eikä tämä johtokaan nyt ihan oikein mene:

To derive the formula, we can use integration by parts, which states: $$ \int u \, dv = uv - \int v \, du $$ 1. Let $u = f(x)$ and $dv = g(x) \, dx$.
2. Differentiate $u$ to get $du = f'(x) \, dx$.
3. Integrate $dv$ to get $v = \int g(x) \, dx$.

Substitute into the integration by parts formula:

$$ \int_{a}^{b} f(x)g'(x) \, dx \goodbreak= f(x)g(x) \Bigg|_{a}^{b} \goodbreak- \int_a^b f'(x)g(x) \, dx $$

Rearrange to isolate $\int_{a}^{b} f'(x)g(x) \, dx$:

$$ \int_{a}^{b} f'(x)g(x) \, dx \goodbreak= f(b)g(b) - f(a)g(a) \goodbreak- \int_{a}^{b} f(x)g'(x) \, dx $$

And we have derived the partial integration formula.

Tästä ei voi antaa kuin 0 pistettä.

Olin aikeissa kommentoida, että vain tekoäly voisi palauttaa tällaisen “ratkaisun”. Lahtisen mukaan kuitenkin “Jotkut ottivat lähtökohdaksi vastaavan määräämättömien integraalien kaavan. Siitä ei saanut pisteitä.” Luulen, että näin vastanneet kokelaat ovat kyllä tienneet ettei kyseessä ole ratkaisu, mutta kun eivät ole osanneet kaavaa johtaakaan, ovat kokeilleet saisiko taulukkokirjasta löytyvää kaavaa ja analyysin peruslausetta soveltamalla säälipisteitä. ChatGPT:lle en kykene attribuoimaan säälipisteiden yrittämistä, vaan papukaija nyt vain on laittanut sanoja peräkkäin.

Tässä kohtaa vähän harmittaa, koska esikokeiluissani sain alkeellisemmalla kehotteella pelkällä kuvantunnistusmallilla oikein hyvän todistuksen, joka alkaa tulon derivaatan kaavasta $(uv)' = u'v + uv'$, mutta sitten varsinaisella koekerralla hienommalla kehotteella malli epäonnistui.

Tehtävä 8: nouseva saari

The island is circular in shape, and its diameter in the year 1995 is 110 m. The base of the island declines uniformly by 72 cm when measured horizontally for every ten meters. The land rises by 38 cm every hundred years. Derive the expression $A(t)$ for the island’s area (area in square meters and time t in years). By how many percent is the island’s area larger in the year 2000 than in 1995? During which year, between the years 1995 and 2300, does the island’s area increase the most?

Käännös menee ihan hyvin, entäs ratkaisu?

The area of a circle is given by $A = \pi r^2$, where $r$ is the radius of the circle. The radius of the island in 1995 is $\frac{110}{2} = 55 \, \text{m}$.

1. Decline in Base: The base of the island declines by $72 \, \text{cm}$ every ten meters, so for every meter, it declines by $\frac{72}{10} = 7.2 \, \text{cm}$ or $0.072 \, \text{m}$. This happens in 100 years, so every year the decline is $\frac{0.072}{100} = 0.00072 \, \text{m/year}$.

2. Rise in Land: The land rises by $38 \, \text{cm}$ every 100 years, which is $0.38 \, \text{m}$ in 100 years. This is $\frac{0.38}{100} = 0.0038 \, \text{m/year}$.

3. Net Change: The net yearly change in radius is $0.0038 - 0.00072 = 0.00308 \, \text{m/year}$.

Tässä ChatGPT ei hahmota tilannetta ollenkaan: pohjan tasainen viettäminen kertoo maan korkeudesta saaren keskipisteestä mitatun etäisyyden funktiona, kun taas maanpinnan kohoaminen on ajassa tapahtuva muutos. ChatGPT tulkitsee, että nämä ovatkin kaksi ajassa tapahtuvaa prosessia, joiden yhteisvaikutus voidaan laskea erotuksena 0,38 cm/a - 0,0072 cm/a (kymmenen metriä ja sata vuotta näyttävät johtavan lukuarvojen jakamiseen kymmenellä ja tuhannella). Näin hölmöön virheeseen tarvitaan kone, ihminen ei siihen kykenisi. (Ihminen ei tosin välttämättä kykene myöskään oikeaan ratkaisuun. Lahtisen mukaan lähes 1700 kokelasta ei jättänyt ratkaisua ollenkaan ja vain 760 sai tehtävästä täydet pisteet.¹)

Pinta-alan kasvunopeuden perustelusta annan 1 pisteen, koska Lahtisen mukaan monet ihmiskokelaat olivat perustelleet sen puutteellisesti esimerkiksi intuitioon vetoamalla, kun taas ChatGPT:n vastaus ei käytä oikopolkuja. Sen kaavoissa on väärät lukuarvot, mutta ne ovat oikeaa muotoa:

Year with Maximum Area Increase between 1995 and 2300

To find the year when the island’s area increases the most, we need to find the maximum of the rate of change of $A(t)$, which is $\frac{dA}{dt}$.

The derivative $\frac{dA}{dt}$ can be found as follows: $$ \frac{dA}{dt} = \frac{d}{dt} \left[ \pi \left( 55 + 0.00308t \right)^2 \right] $$ We need to find the year $t$ when $\frac{dA}{dt}$ is at its maximum between 1995 and 2300, or $t$ between 0 and 305. We can use calculus to find this maximum by setting the second derivative $\frac{d^2A}{dt^2}$ equal to zero and solving for $t$.

The first derivative of $A(t)$ is $\frac{dA}{dt} = 3025\pi \left( 6.272 \times 10^{-9} t + 0.000112 \right)$.

The second derivative of $A(t)$ is $\frac{d^2A}{dt^2} = 1.89728 \times 10^{-5} \pi$.

Since the second derivative is a constant and greater than zero, this implies that the function $A(t)$ is concave up for all $t$. Therefore, the rate of change $\frac{dA}{dt}$ will keep increasing as time passes.

So, the island’s area will increase the most in the year 2300 among the years between 1995 and 2300.

Tehtävä 9: etäisyys kompleksitasossa

(a) At the time $t \geq 0$, there are points $z_1 = z_1(t)$ and > $z_2 = z_2(t)$ in the complex plane at the positions $$ z_1(t) = t + ie^{-t} $$ $$ z_2(t) = 3 + t + 2ie^{-t} $$

Determine the distance between the points $|z_1 - z_2|$ at time $t$. When is the distance the largest? Determine $\lim_{{t \to \infty}} |z_1(t) - z_2(t)|$.

(b) When $a \in [0, 2]$, let $f(a)$ denote the smallest value of the function $g(x) = x^2 - 2ax$ in the interval [1, 4]. Define the function $f$ and draw its graph. Determine the derivative $f'( \frac{3}{2} )$. Does $f$ have a derivative in every point of the interval [0, 2]?

ChatGPT valitsee tehtävän (a) ja tekee heti alussa laskuvirheen:

Step 1: Finding $|z_1 - z_2|$

To find the distance between $z_1$ and $z_2$ at time $t$, we need to find $|z_1 - z_2|$. $$\begin{aligned} z_1 - z_2 &= (t + ie^{-t}) - (3 + t + 2ie^{-t}) \\ &= (t - t) + i(e^{-t} - 2e^{-t}) \\ &= -i(e^{-t}) \\ |z_1 - z_2| &= |-i(e^{-t})| \\ &= |e^{-t}| \\ &= e^{-t} \end{aligned} $$

Erotuslausekkeen reaaliosasta unohtuu kolmonen. Saatu etäisyys $e^{-t}$ on helpompaa muotoa kuin oikea etäisyys $\sqrt{9+e^{-2t}}$, joten vaikka loppuosassa on ihan kelpoja perusteluita löydetyn kaavan suurimmasta arvosta ja raja-arvosta, annan tästä 0 pistettä. Tämäkin jää vähän harmittamaan, koska esikokeiluissa tämä näytti helpolta tehtävältä, kuten onkin jos kompleksilukujen laskusäännöt ovat tuttuja.

Tehtävä 10: funktion keksiminen

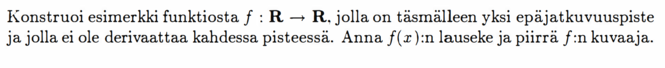
Construct an example of a function $f : R \rightarrow R$, which has exactly one point of discontinuity and which does not have a derivative at two points. Provide the expression for $f(x)$ and draw the graph of $f$.

Tehtävä oli suosikkini kokeessa. Jouduin kyllä lukemaan sen pariin kertaan varmistuakseni, että siinä pyydettiin niin yksinkertaista asiaa kuin näyttikin eikä esimerkiksi surjektiota. ChatGPT suoriutuu kohtalaisesti:

To meet the given conditions, we need to carefully design our function. Here are the steps to construct such a function:

1. Discontinuity: We can create a function that is discontinuous at one point, say $x = 0$, by defining a piecewise function that behaves differently at that point.

2. Lack of Derivative: To make sure the function does not have a derivative at two points, we can incorporate a sharp turn (cusp) at some point $x = a$ where $a \neq 0$. At a sharp turn, the derivative does not exist.

Based on these considerations, let’s define $f(x)$ as follows: $$ f(x) = \begin{cases} x^2, & \text{if } x < 0 \\ 1, & \text{if } x = 0 \\ x, & \text{if } 0 < x < 1 \\ (x-1)^2 + 1, & \text{if } x \geq 1 \end{cases} $$

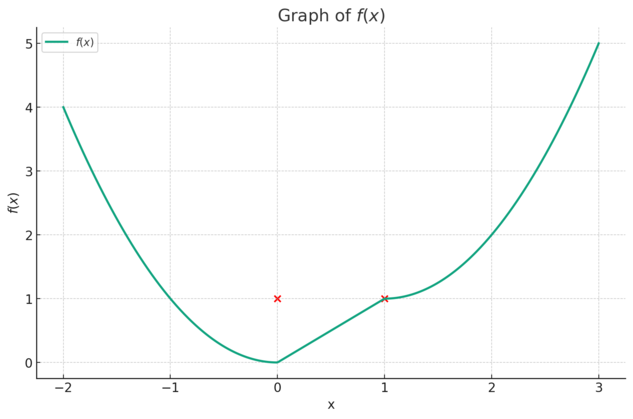
1. Discontinuity: $f(x)$ is discontinuous at $x = 0$ since the limit from the left is $0$ while the function value is $1$.

2. Lack of Derivative:

   • At $x = 0$, the function changes abruptly, so the derivative does not exist.
   • At $x = 1$, the function has a sharp turn (cusp), so the derivative does not exist there as well.

   Thus, this function satisfies both conditions.

Kuvassa voisi vähän enemmän korostaa epäjatkuvuutta nollassa, mutta funktion arvo on merkitty rastilla joten menköön. Perustelut jäävät vähän ohuiksi: hyväksyn perustelun sille, että konstruoitu funktio on nollassa epäjatkuva, mutta lisäksi pitäisi todistaa se jatkuvaksi ja ei-derivoituvaksi ykkösen kohdalla. Tästä ChatGPT sanoo olennaisesti, että se näkyy kuvasta. Annan pitkin hampain 5 pistettä.

Miten kävi?

ChatGPT sai epävirallisessa arvostelussani 32 pistettä, jolla arvosanaksi olisi tullut cum laude approbatur. Tuloksella se ei olisi luultavasti päässyt suoraan esimerkiksi Helsingin yliopistoon opiskelemaan matematiikkaa vaan olisi joutunut kiertämään pääsykokeen kautta.

Vastaukset kokonaisuudessaan löytyvät liitteestä, joka on mahdollisimman lähellä ChatGPT:n tulostetta. Hieman sitä piti muokata, ensinnäkin kaikkien eri ajokertojen yhdistämiseksi ja toiseksi, koska ChatGPT:n tulostama Markdown-formaatti ei kaikissa kohdin sopinut käyttämääni ohjelmaan.

Vastausten kieliasu ja käsiala ovat huomattavan hyviä verrattuna useimpiin ihmisten kirjoittamiin koevastauksiin, joita olen joskus tullut lukeneeksi. Yllättävänä poikkeuksena oli tehtävän 6 kuva. ChatGPT käytti Matplotlib-kirjaston mplot3d-pakettia, joka on jokseenkin rajoittunut.

Kielimalli on stokastinen, jos kohta niin ovat ihmisetkin. Kun kokeilin sen eri moodeja ja erilaisia kehotteita, osaan tehtävistä tuli vaihtelevasti hyviä tai huonoja ratkaisuja. Esimerkiksi tehtävän 7 hölmöily tuntui liittyvän pidempään kehotteeseen, kun taas tehtävässä 10 edistyneempi kehote oli eduksi.

Tehtävän 1 virheluenta toistui usein, mutta jos virhettä ei tapahtunut, loppuosassa oli usein jokin virhe — ratkaistavaksi tulee toisen asteen yhtälö $4x^2-17x+18=0$, joka on ilmeisesti mallille liian hankala päässälaskuksi.

Muissakaan tehtävissä malli ei aina ymmärrä ”käyttää laskinta” eli kirjoittaa ja ajaa Python-koodia, tai jos ymmärtää, tuloksena ei ole tarkka arvo kuten $\sqrt 6/4$ vaan likiarvo 0,6124. Tämä vähän ihmetyttää, koska malli osaa kuitenkin käyttää sympy-kirjastoa, joka vastaa symbolista laskinta.

Saaritehtävään 8 en saanut kelvollista ratkaisua millään yrittämällä. Oppilaille usein annettava neuvo on piirtää tilanteesta kuva, mutta en saanut kohtuullisella yrittämisellä hyödyllistä kuvaa tilanteesta. Yritin myös piirtää itse havainnollisen kuvan ja tarjota sitä ChatGPT:lle, mutta ei sekään auttanut.

Jos eri kokeiluista saadut parhaat ratkaisut yhdistettäisiin samaan koepaperiin, arvosana voisi hyvinkin olla laudatur. Tätäkin voisi yrittää esimerkiksi Langchain-kirjastolla: pyydetään mallilta monta eri ratkaisua ja sitten annteen mallia itse vertailla, mikä niistä tuntuu parhaalta. Samaten malli voisi katsella ja arvioida ratkaisujensa sisältämiä kuvia, mikä olisi kenties auttanut tehtävässä 6. OpenAI:n API ei kuitenkaan vielä sisällä kuvia ymmärtävää mallia, mikä olisi tarpeen suunnitelman toteuttamiseksi. API:n täydentyminen on kuitenkin vain ajan kysymys.

Pystyisikö ChatGPT:llä huijaamaan ylioppilaskokeessa? Varmaan pystyisi, jos sinne voisi salakuljettaa ChatGPT-sovelluksen vaikka puhelimessa tai omalla tietokoneellaan. Tietoliikennettä varmaan osataan valvoa niin hyvin, että tästä jäisi kiinni. Jos joku hakkeri onnistuisi ajamaan omalla koneellaan paikallista kielimallia (ja saisi tilanteen näyttämään siltä, että kone on käynnistetty Abitti-järjestelmään) niin tämäkään ei ihan riittäisi. Parhaatkaan nykyiset omalla koneella ajettavat mallit eivät nimittäin osaa ainakaan suomea riittävän hyvin. Ajan kysymys voi olla tämäkin.

Pystyykö tällä tavoin huijaamaan kotitehtävissä? Ihan helposti, ja vilppiä tapahtuu jo.

Voisiko ChatGPT toimia matematiikan apuopettajana? Varmaankin voisi, kunhan sitä käyttää järkevästi. Ilmeinen mutta oppimiselle haitallinen tapa olisi käyttää tekoälyapuria tehtävien ratkaisemiseen. Parempi olisi kokeilla, saako sen antamaan sopivia vihjeitä, joilla pääsee ratkaisussa eteenpäin ilman että koko ratkaisu paljastuu. Khan Academyn Khanmigo näyttäisi olevan tämäntapainen apuri, ja edellä linkitetty Ylen uutinen mainitsee Suomessa kehitteillä olevan Assarin. Yhtenä ratkaistavana ongelmana tällaisissa apureissa on, että tekoäly voi sepittää uskottavan näköistä mutta täysin virheellistä tekstiä. Saaritehtävän ja osittaisintegrointitehtävän ”ratkaisut” ovat tästä hyviä esimerkkejä.

Viekö ChatGPT matemaatikkojen työpaikat ja hallitseeko se ihmiskunnan tulevaisuuden? Ei tietenkään vielä, mutta hermostuneisuutta aiheuttava kysymys on, miten kielimallien kehitys jatkuu. Jos nyt asetetaan ihmisyyden kovan ytimen raja magnaan tai varmuuden vuoksi laudaturiin, niin mitä joudutaan sanomaan sitten jos ChatGPT yltää siihen vaikka puolen vuoden päästä? Uusi teknologia tapaa seurata S-käyrää, jolla se kehittyy ensin nopeasti, jolloin optimistit uskovat teknologian muuttavan kaiken — mutta sitten kehitys tasaantuu, jolloin pessimistit pääsevät muistuttamaan että niinhän he sanoivat.

Käyrän tasaantumisesta ei vielä näy merkkejä, joten kehityksessä oltaneen alkuvaiheessa, jolloin asymptootin y-koordinaatin ennustaminen on kovin vaikeaa.

Kehote: Illustrate the S curve of the capability of new technologies, especially how difficult it is to predict the eventual level reached from the initial part of the curve. For example, plot multiple curves that have nearly indistinguishable initial segments but wildly different long-term behavior, including curves that start out lower and end up higher, and vice versa. Use the xkcd style when plotting to emphasize the qualitative nature of the plot, and omit unnecessarily detailed axis labels and legends.

Muualla

Timo Tossavainen on yrittänyt saada ChatGPT:ltä todistuksen Bolzanon—Weierstrassin lauseelle, eikä todistus mennyt ihan oikein. Simo Kivelä on kokellut ChatGPT:tä geometrian tehtävässä ja Wolfram Language -ohjelman tuottamisessa, samoin vähän epätäydellisin tuloksin.

OpenAI väittää GPT-4:n saaneen hyvät pisteet SAT-kokeesta, joka lienee Yhdysvaltain lähin vastine meidän ylioppilaskokeellemme. Käsittääkseni SAT:n matematiikan tehtävät ovat osittain monivalintatehtäviä ja osittain sellaisia, joissa pitää kirjoittaa vain lopputuloksena saatava lauseke tai lukuarvo. Tämä ei tarkoita, että ne ovat helppoja, mutta niissä ei jää kiinni huonoista perusteluista.

Yksi kiintoisa tapa käyttää kielimalleja on tuottaa todistusyritelmiä, jotka voidaan tarkastaa koneellisesti. Tällaiseen tarkastamiseen soveltuvat formaalit kielet ovat ihmiselle varsin raskaita — esim. Terence Tao on kuvannut ongelmaa niin, että aivan ilmeiset todistusaskeleet ovat hyvin vaikeita formalisoida. Tähän tylsään työhön kärsivällinen kielimalli voisi sopia oikein hyvin, ja myös Tao vaikuttaa optimistiselta.

OpenAI on raportoinut jo vuonna 2022, että sen kielimalli (joka ilmeisesti ei ole mikään julkisesti saatavilla oleva versio vaan tätä varten erikseen opetettu) on ratkonut onnistuneesti joitakin koululaisten matematiikkakilpailujen tehtäviä. Silti tutkijat joutuivat toteamaan, että malli ei vielä kykene pitkiin päättelyketjuihin eikä rutiininomaisesti ratkomaan tehtäviä parhaiden ihmisten tasolla:

Despite our models’ capability […] we believe that their current main limitation lies in their inability […] to chain more than 2 or 3 non-trivial steps of mathematical reasoning, preventing them from consistently (instead of exceptionally) solving challenging olympiad problems. We’ve been repeatedly impressed by the complexity of some of the proofsteps generated by our models. But, proofs requiring many of such reasoning steps remain beyond our current compute horizon. Even if we solved a selection of challenging olympiad problems, our models are still very far from being competitive with the brightest students in these competitions.

Saa nähdä, onko pitkien päättelyketjujen tuottaminen kielimalleille olennainen ongelma vai ratkeaako se yhtä yllättävästi kuin luontevan luonnollisen kielen tuottaminen. Ainakin niiden tutkimiseen näkyy nyt liikenevän resursseja.